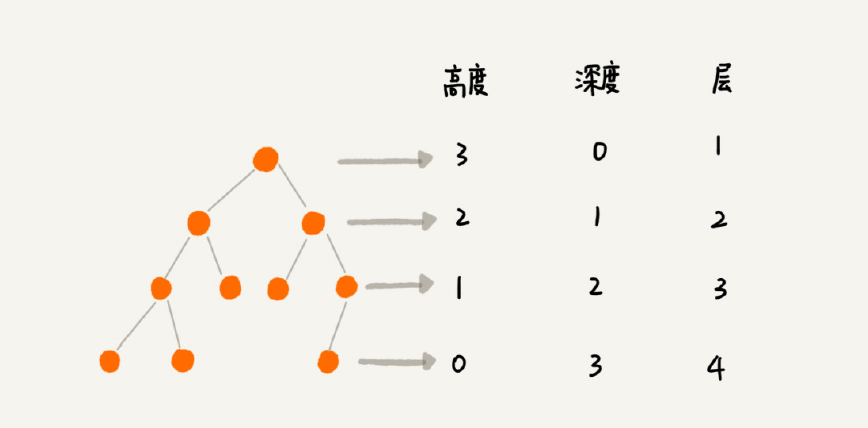
二叉树
树
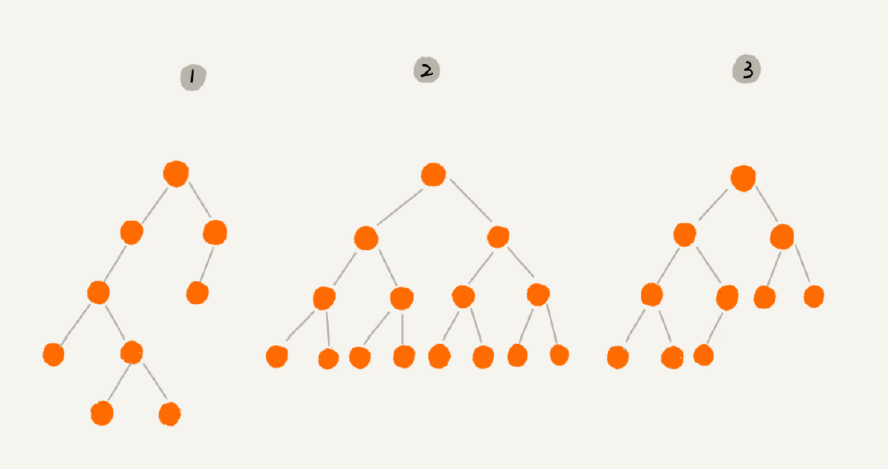
表示、存储一棵二叉树
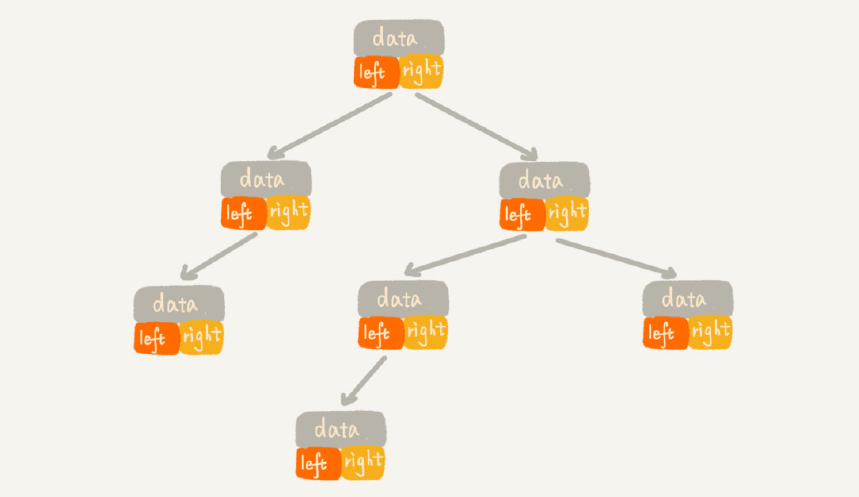
链式存储法
每个结点有三个字段,其中一个存储数据,另两个是指向左右子节点的指针。
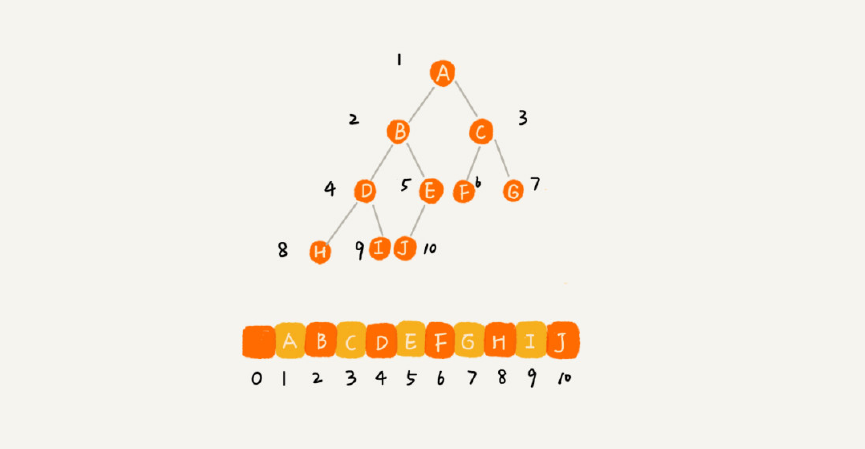
顺序存储法(基于数组)
根节点存储在下标i=1的位置,左子节点存储在下标2i=2的位置,右子节点存储在2i+1=3的位置,以此类推。
如果节点 X 存储在数组中下标为 i 的位置,下标为 2 i 的位置存储的就是左子节点,下标为 2 i + 1 的位置存储的就是右子节点。
我们只要知道根节点存储的位置,这样就可以通过下标计算,把整棵树都串起来。
为了方便计算子节点,根节点会存储在下标为 1 的位置
二叉树的遍历
前序遍历
对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
中序遍历
对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
后序遍历
对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
层序遍历
从树的第一层开始从左到右打印节点
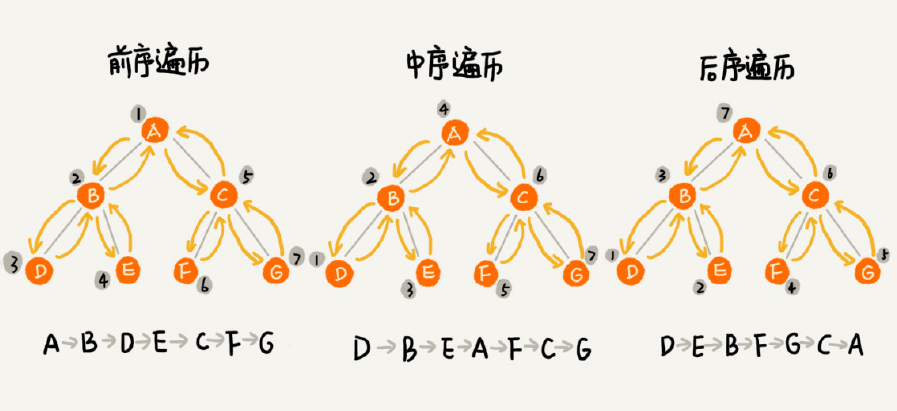
实际上,二叉树的前、中、后序遍历就是一个递归的过程。
比如,前序遍历,其实就是先打印根节点,然后再递归地打印左子树,最后递归地打印右子树。
二叉树以及二叉树遍历代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
|
public class BinaryTree {
private Node root;
private int data = 0;
private int size = 0;
public BinaryTree() {
root = new Node(data);
}
public void add(int data) {
if (size == 0) {
root.data = data;
size++;
} else {
add(root, new Node(data));
}
}
private void add(Node root, Node newNode) {
if (root == null) {
return;
}
if (newNode.data < root.data) {
if (root.leftNode == null) {
root.leftNode = newNode;
size++;
} else {
add(root.leftNode, newNode);
}
} else {
if (root.rightNode == null) {
root.rightNode = newNode;
size++;
} else {
add(root.rightNode, newNode);
}
}
}
public int getLow() {
Node parent = root;
while (parent.leftNode != null) {
parent = parent.leftNode;
}
return parent.data;
}
public int getHigh() {
Node parent = root;
while (parent.rightNode != null) {
parent = parent.rightNode;
}
return parent.data;
}
public void preOrder() {
System.out.println("前序遍历:");
pre(root);
System.out.println(" ");
}
private void pre(Node node) {
if (node != null) {
System.out.print(node.data + " ");
pre(node.leftNode);
pre(node.rightNode);
}
}
public void inOrder() {
System.out.println("中序遍历:");
in(root);
System.out.println(" ");
}
private void in(Node node) {
if (node != null) {
in(node.leftNode);
System.out.print(node.data + " ");
in(node.rightNode);
}
}
public void postOrder() {
System.out.println("后序遍历:");
post(root);
System.out.println(" ");
}
private void post(Node node) {
if (node != null) {
post(node.rightNode);
post(node.leftNode);
System.out.print(node.data + " ");
}
}
private class Node {
private int data;
private Node leftNode;
private Node rightNode;
public Node(int data) {
this.data = data;
this.leftNode = null;
this.rightNode = null;
}
}
public static void main(String[] args) {
System.out.println("*************");
BinaryTree t = new BinaryTree();
t.add(40);
t.add(25);
t.add(78);
t.add(10);
t.add(32);
t.add(50);
t.add(93);
t.add(3);
t.add(17);
t.add(30);
t.add(38);
System.out.println(t.getLow());
System.out.println(t.getHigh());
System.out.println("Size-" + t.size);
System.out.println(t);
t.inOrder();
t.preOrder();
t.postOrder();
}
}
|
二叉查找树 Binary Search Tree
二叉查找树的定义
二叉查找树又称二叉搜索树。其要求在二叉树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树的节点的值都大于这个节点的值。
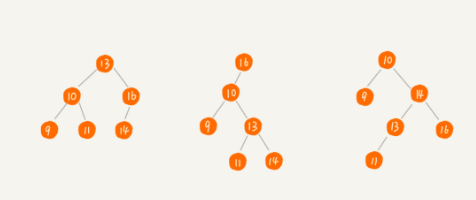
二叉查找树的查找操作
二叉树类、节点类以及查找方法的代码实现
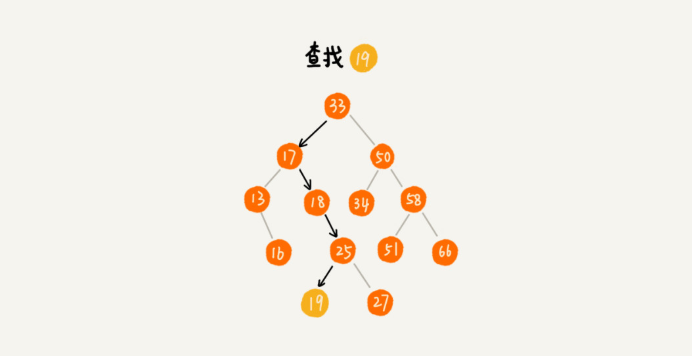
先取根节点,如果它等于我们要查找的数据,那就返回。
如果要查找的数据比根节点的值小,那就在左子树中递归查找;
如果要查找的数据比根节点的值大,那就在右子树中递归查找。
1
2
3
4
5
6
7
8
9
10
11
12
13
| public Node find(int data) {
Node p = tree;
while (p != null) {
if (data < p.data) {
p = p.left;
} else if (data > p.data) {
p = p.right;
} else {
return p;
}
}
return null;
}
|
二叉查找树的插入操作
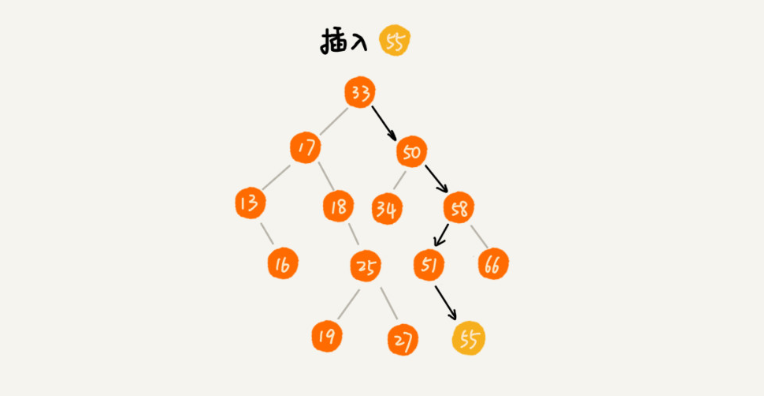
新插入的数据一般都是在叶子节点上,所以我们只需要从根节点开始,依次比较要插入的数据和节点的大小关系。
如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。
同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public void insert(int data) {
if (tree == null) {
tree = new Node(data);
return;
}
Node p = tree;
while (p != null) {
if (data < p.data) {
if (p.left == null) {
p.left = new Node(data);
return;
}
p = p.left;
} else {
if (p.right == null) {
p.right = new Node(data);
return;
}
p = p.right;
}
}
}
|
二叉查找树的删除操作
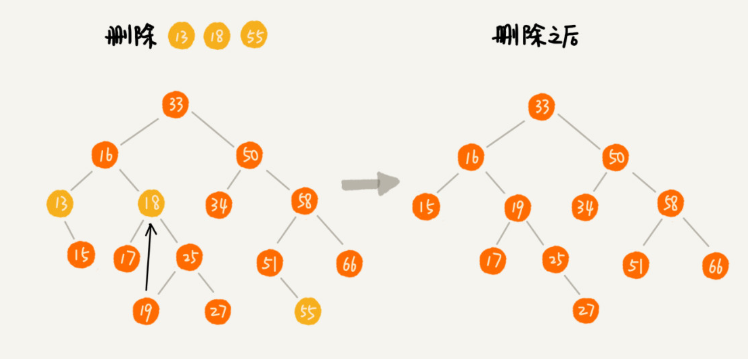
第一种情况,删除的节点没有子节点直接将其父节点指向置为null。
第二种情况,删除的节点只有一个子节点,将其父节点指向其子节点。
第三种情况,删除的节点有两个子节点,首先找到该节点右子树中最小的的节点把他替换掉要删除的节点 然后再删除这个最小的节点,该节点必定没有子节点,否则就不是最小的节点了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
public void delete(int data) {
Node p = root;
Node pp = null;
while (p != null && p.data != data) {
pp = p;
if (data < p.data) {
p = p.left;
} else {
p = p.right;
}
}
if (p == null) {
return;
}
if (p.left != null && p.right != null) {
Node minP = p;
Node minPP = pp;
while (minP.left != null) {
minPP = minP;
minP = minP.left;
}
p.data = minP.data;
p = minP;
pp = minpp;
}
Node child;
if (p.left != null) {
child = p.left;
} else if (p.right != null) {
child = p.right;
} else {
child = null;
}
if (pp == null) {
root = child;
} else if (pp.left == p) {
pp.left = child;
} else {
pp.right = child;
}
}
|
关于二叉查找树的删除操作,还有个非常简单、取巧的方法,就是单纯将要删除的节点标记为“已删除”,但是并不真正从树中将这个节点去掉。
这样原本删除的节点还需要存储在内存中,比较浪费内存空间,但是删除操作就变得简单了很多。而且,这种处理方法也并没有增加插入、查找操作代码实现的难度。
二叉查找树的其他操作
二叉查找树中还可以支持快速地查找最大节点和最小节点、前驱节点和后继节点。
二叉查找树除了支持上面几个操作之外,还有一个重要的特性,就是中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是 O(n),非常高效。因此,二叉查找树也叫作二叉排序树。
支持重复数据的二叉查找树
前面的二叉查找树的操作,我们默认树中节点存储的都是数字,针对的都是不存在键值相同的情况。
我们可以通过两种办法来构建支持重复数据的二叉查找树。
第一种方法
二叉查找树中每一个节点不仅会存储一个数据,因此我们通过链表和支持动态扩容的数组等数据结构,把值相同的数据都存储在同一个节点上。
第二种方法
每个节点仍然只存储一个数据。在查找插入位置的过程中,如果碰到一个节点的值,与要插入数据的值相同,我们就将这个要插入的数据放到这个节点的右子树,也就是说,把这个新插入的数据当作大于这个节点的值来处理。
当要查找数据的时候,遇到值相同的节点,我们并不停止查找操作,而是继续在右子树中查找,直到遇到叶子节点,才停止。这样就可以把键值等于要查找值的所有节点都找出来。
对于删除操作,我们也需要先查找到每个要删除的节点,然后再按前面讲的删除操作的方法,依次删除。
二叉查找树的时间复杂度分析
最坏、最好情况
如果根节点的左右子树极度不平衡,已经退化成了链表,所以查找的时间复杂度就变成了 O(n)。
最理想的情况,二叉查找树是一棵完全二叉树(或满二叉树)。不管操作是插入、删除还是查找,时间复杂度其实都跟树的高度成正比,也就是 O(height)。而完全二叉树的高度小于等于 log2n。
平衡二叉查找树
我们需要构建一种不管怎么删除、插入数据,在任何时候都能保持任意节点左右子树都比较平衡的二叉查找树,这就是一种特殊的二叉查找树,平衡二叉查找树。
平衡二叉查找树的高度接近 logn,所以插入、删除、查找操作的时间复杂度也比较稳定,是O(logn)。
二叉查找树相比散列表的优势
散列表中的数据是无序存储的
如果要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历就可以在 O(n) 的时间复杂度内,输出有序的数据序列。
散列表扩容耗时很多
而且当遇到散列冲突时,性能不稳定,尽管二叉查找树的性能不稳定,但是在工程中,我们最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在 O(logn)。
散列表存在哈希冲突
尽管散列表的查找等操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个常量不一定比 logn 小,所以实际的查找速度可能不一定比 O(logn) 快。
加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。
散列表装载因子不能太大
为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
综合这几点,平衡二叉查找树在某些方面还是优于散列表的,所以,这两者的存在并不冲突。